登录/ 注册
 找回密码
 立即注册
关闭

CSDN热搜

程序园 精品问答 技术交流 资源下载
返回列表 发新帖
首页 › 业界区 › 业界 ›探秘Transformer系列之（16）--- 资源占用

探秘Transformer系列之（16）--- 资源占用

悯拄等 4 天前
探秘Transformer系列之（16）--- 资源占用


目录

  • 探秘Transformer系列之（16）--- 资源占用

    • 文章总表
    • 0x00 概述
    • 0x01 背景知识

      • 1.1 数据类型
      • 1.2 进制&换算

        • 数字进制
        • 存储度量
        • 换算

      • 1.3 参数显存占用

        • 有参数的层
        • 无参数的层
        • 所需资源

      • 1.4 计算量

    • 0x02 Transformer参数量

      • 2.1 术语
      • 2.2 embedding层
      • 2.3 Transformer层

        • MHA
        • FFN
        • LayerNorm
        • 小结

      • 2.4 lm_head
      • 2.5 最终参数量
      • 2.6 LLaMA3

        • SwiGLU
        • GQA


    • 0x03 Transformer显存占用

      • 3.1 训练
      • 3.2 推理
      • 3.3 激活

        • 架构
        • 术语说明
        • 数据量

          • 注意力块
          • MLP
          • LayerNorm
          • 总结
          • 并行



    • 0x04 Transformer计算量

      • 4.1 矩阵乘法
      • 4.2 前向传播计算量

        • Embedding
        • MHA

          • 计算Q、K、V
          • QK^T
          • 乘以V
          • 线性映射

        • MLP
        • LayerNorm
        • 单层layer

      • 4.3 综合思考

        • 反向传播

          • 单层
          • logits

        • 总体计算量

      • 4.4 计算特点

        • 与参数量的关系

          • 单次推理
          • 单次训练

        • 带宽受限

          • 注意力计算
          • FFN计算

        • KV Cache的影响

          • prefill
          • decode
          • 总体
          • kv cache 节省了多少计算量



    • 0x05 优化方向

      • 5.1 基于注意力机制来修改外推技术
      • 5.2 基于Memory机制外推技术

    • 0xFF 参考


文章总表

全部文章列表在这里 探秘Transformer系列之文章列表，后续每发一篇文章，会修改这里。
0x00 概述

对于标准 Transformer 模型，不管是 Encoder Only 的 Bert 系列模型，还是 Decoder Only 的 GPT 系列模型，同配置下参数量和计算量都是类似的。其中的一个关键点是：标准 Transformer block（层）输入、输出以及中间 Hidden Dim 保持不变，始终是 Token Embedding 的 Hidden Dim，所有的 Transformer Block 都非常规整。
如下图所示，Encoder主要参数都来自几个矩阵乘的 Weight 矩阵，其中 d 表示 Token Embedding 的 Hidden Dim，l 表示 Token 数，h 表示 MHA 中的 Head 个数，\(d_{FFN}\) 表示 FFN 层中间升维后的 Dim。其主要几个模块的参数量如下。

  • MHA：\(W_Q，W_K，W_V\) 的大小都是 d x d。当然这里也可以从 h 个 Head 的角度去看，则每个 Head 的 \(W_Q，W_K，W_V\)  为 d x d/h。在 MHA 的最后还有一个矩阵乘操作，对应的 \(W_{out}\) 维度依然为 d x d。所以MHA处权重矩阵的参数量是 \(3d \times d + d \times d\)。
  • FFN：标准 Transformer 的 FFN 中有两个 Linear 层（先升维再降维），对应权重矩阵 \(W_1\) 和$ W_2$ 的大小都是 \(d_{FFN}\) x d，并且标准的 \(d_{FFN}\) 为 4d，也就是说 FFN 处两个权重矩阵的参数量为 8d x d。
1.jpeg

综上，在标准的 Transformer 模型或者 LLaMA 系列（MHA）中，如果忽略词表、Embedding、LayerNorm 等参数后，总参数量为（所有 Transformer Block）： \(N = n_{layer} \times (n_{mha}+ n_{ffn}) = n_{layer} \times (3d \times d + d \times d + 8d \times d) = 12 \times n_{layer} \times d \times d\)
注意：本章参考了多篇论文，其中对术语的定义各不相同，因为模型结构也不同，所以计算结果与其它资料可能也有差异。
0x01 背景知识

1.1 数据类型

深度学习中用的数值类型命名规范一般为TypeNum，比如Int64、Float32、Double64。

  • Type：有Int，Float，Double等。
  • Num: 一般是 8，16，32，64，128，表示该类型所占据的比特数目。
常用的数值类型如下图所示。
类型大小（字节数）int40.5int81int162int324int648float324float1621.2 进制&换算

我们先抛出一个问题:1B参数对应多少G显存？B和G都代表十亿（1000M或1024M），但这是两个不同的度量维度。
数字进制

B是英美常用的进制单位，比如：

  • 1K = 1000，一千；
  • 1M = 1000 K，百万；
  • 1B = 1000 M，十亿；
可以看出来，这个进制单位以 1000 为进制。以 Qwen-7B 为例，7B 的意思就是 这个 LLM 的 模型参数有 70亿 个 参数。
存储度量

G是计算机内存/磁盘存储的度量，基本单位是字节，进制是 1024。单位依次是：KB / MB / GB / TB。平时说显存有多少G/M是说有多少G/M个字节（byte），1个字节=8比特（bit）。举例来说：有一个1000x1000的 矩阵，float32，那么占用的显存差不多就是1000x1000x4 Byte = 4MB。
换算

可以看出来，\(1B=10^9 byte \approx 1GB\)，1B和1G的大小基本一致，所以我们记作B和G相等。但是，1B模型参数对应多少G内存和参数的精度有关。如果是全精度训练（fp32），一个参数对应32比特，也就是4个字节，参数换算到显存的时候要乘4，也就是1B模型参数对应4G显存。如果是fp16或者bf16就是乘2，1B模型参数对应2G显存。具体如下表所示。
数据类型每1B参数需要占用内存fp324Gfp16/bf162Gint81Gint40.5G1.3 参数显存占用

有参数的模块才会占用显存。这部份的显存占用和输入无关，模型加载完成之后就会占用。一般的卷积层都会占用显存，而我们经常使用的激活层Relu没有参数，所以不会占用缓存。
有参数的层

常见的有参数的模块主要包括：

  • 卷积层，通常的conv2d。
  • 全连接层，也就是Linear层。
  • BatchNorm层。
  • Embedding层。
无参数的层

常见的无参数的模块主要包括：

  • 多数的激活层，比如Sigmoid/ReLU。
  • 池化层。
  • Dropout。
所需资源

我们可以用如下公式来计算神经网络的显存占用：显存占用 = 模型显存占用 + 输入输出相关的显存
模型显存占用是模型中与输入无关的显存占用，主要包括：

  • 模型权重参数。
  • 梯度（一般是参数量的1倍）。
  • 优化器的动量（和具体优化器密切相关，比如普通SGD没有动量，momentum-SGD动量与梯度一样，Adam优化器动量数量是梯度的两倍）。
输入输出相关的显存占用主要如下：

  • batch_size × 每个样本的显存占用。
  • 每一层的feature map，需要保存激活来进行反向传播。
因为 反向传播 / Adam-优化 / Transformer架构 等因素，一般来说，训练需要的显存，是 同样规模推理 的 3-4倍。
1.4 计算量

上文提到Transformer的计算复杂度是 $O(dN^2) $。大 O 表示法关注的是计算量级与输入规模之间的关系，并不是具体的计算量。具体计算量通常用FLOPs体现。这里简单列举一些比较常见的单位：

  • FLOPs ：floating point of operations的缩写，是浮点运算次数，一般特指乘加运算次数，理解为计算量，可以用来衡量算法/模型复杂度。
  • 一个GFLOPS（gigaFLOPS）= 每秒十亿（=10^9）次的浮点运算
  • 一个TFLOPS（teraFLOPS） = 每秒一万亿（=10^12）次的浮点运算
0x02 Transformer参数量

以Decoder only模型为例，其主要包括 3 个部分：embedding，decoder，head。最主要部分是decoder，其由若干个decoder-layer组成，每个decoder-layer又分为两部分：MHA和FFN。我们接下来逐一看看这些模块的参数量。
2.1 术语

我们先给出本节使用的术语。
SymbolMeaning\(d\)模型的词嵌入大小（The model size / hidden state dimension / positional encoding size）\(h\)注意力头个数\(s\)文本总长度（prompt+解码器输出）\(b\)数据batch size（批大小）\(l\)Transformer层数\(v\)词表大小2.2 embedding层

embedding层的输入形状是[b,s,v]，输出形状是[b,s,d]，参数量为\(v \times d\)。如果采用可训练式的位置编码，会有一些可训练模型参数，但是其数量比较少。如果采用相对位置编码，例如RoPE和ALiBi，则不包含可训练的模型参数。因此我们忽略位置编码的参数。
2.3 Transformer层

Transformer模型由 l 个相同的层组成，每个层主要分为两部分：MHA和FFN。因为多头只是逻辑上切分，物理上没有增加模块，因此后续讨论中省略多头（某些论文中如果讨论多头相关，我们会以论文为准），而又因为Decoder only模型使用的是自注意力，因此接下来我们认为 Q、K、V、O的维度相等。
MHA

MHA中包含四个权重矩阵\(W^Q,W^K,W^V,W^O\)以及偏置（某些模型可能没有偏置）。4个权重矩阵的形状为 [\(d\),\(d\)]，4个偏置的形状为 [\(d\)]，其中 \(d = h \times d_{head}\)。因此，多头注意力层参数量为：\(4\times (d \times d + d) = 4d^2 + 4d\)。
FFN

FFN包括两个线性层。

  • 第一层将原有的维度映射到4倍原维度大小，即从\(d\)映射到4\(d\)。权重矩阵形状是[d, 4d]，偏置形状是[4d]。参数量为：\(d\times 4d + 4d\)
  • 第二层从4倍维度降维回原始维度。即从4\(d\)映射到\(d\)。权重矩阵形状是[4d, d]，偏置形状是[d]。参数量为： \(4d\times d + d\)
最终FFN的参数是：\(8d^2 + 5d\)。
LayerNorm

对于Layer Norm来说，其缩放参数 \(\gamma\)与平移参数 \(beta\) 维度都为 \(d\)，因此参数量是 \(2 \times d\)。因为MHA和FFN都有LayerNorm，因此总参数量是\(4 \times d\)。
小结

综上，单个Transformer层的参数量是：\(12d^2 + 13d\)。
2.4 lm_head

lm_head是自然语言处理模型中的一个组件，主要作用是将模型的输出（通常是经过Transformer编码器处理后的隐藏状态）转换成预测下一个词的概率分布。
Head与embedding的参数量相同。如果是tied embedding（即，head权重矩阵与词嵌入矩阵是参数共享的），则两者公用一个参数。
2.5 最终参数量

最终，l 层transformer模型的可训练模型参数量为\(l(12d^2 + 13d) + 2vd\) 。当d较大时，可以忽略一次项，模型参数量近似为\(12ld^2\) 。
2.jpeg

2.6 LLaMA3

我们再用LLaMA3来看看在工业界落地中的一些特殊之处。
SwiGLU

LLaMA 等模型在 FFN 中会使用 SwiGLU 激活，这也就导致其会额外多了一个权重矩阵。LLaMA论文中提到，使用 SwiGLU 后将 dFFN 从 4d 降低到了 8d/3。这样 3 个权重矩阵的参数量还是 8d，总的参数量依然可以使用 \(12 \times n_{layer}\times d\times d\)来 预估。
GQA

前面公式对应的是 MHA（Multi Head Attention），这也是 LLaMA-1 系列模型的标准实现。不过，LLaMA-2 的 30B 和 70B 模型以及 LLaMA-3 的全部模型都开始使用 GQA（Grouped Query Attention）。使用 GQA 时，多个 注意力头会共享一个 Key 和 Value，此时\(W^K,W^V\)的大小会变为 d x d/g，其中 g 表示每 g 个 Head 共享相同的 Key 和 Value。LLaMA 2论文提到，为了保持使用 GQA 和使用 MHA 的总参数量保持不变，对于 GQA 模型，LLaMA 2会将 FFN Dim 维度乘以 1.3。
经过上述调整之后，LLaMA 3 不再是标准的 Transformer Block，此时使用 \(N=12d^2\) 来预估参数量已经不太准确。但依旧可以将其按照（\(W^Q,W^O\)）（\(W^K,W^V\)），$W_{FFN} $和 \(W_{emb}\) 4 个部分来统计。比如，对于 LLaMA 3 模型，我们可以按照下述方式估计其参数量：\(N = n_{layer} \times (2d^2 + 2d \times  d \times  kv/h + 3d \times d_{FFN})+2 \times  Vocab \times  d\)。
0x03 Transformer显存占用

3.1 训练

在训练神经网络的过程中，占用显存的大头主要分为四部分：模型参数、前向计算过程中产生的中间激活、后向传播计算得到的梯度、优化器状态。后面几个的数量可能比模型参数更大，因此对模型内存的需求量也更大。
训练大模型时经常采用AdamW优化器，并用混合精度训练来加速训练，我们基于这个前提分析显存占用。在一次训练迭代中，每个可训练模型参数需要保存这个参数本身、参数对应的梯度以及优化器对这个参数的两个状态（Adam中的一阶动量和二阶动量）。设模型参数量为 Φ ，那么梯度的元素数量为 Φ ，AdamW优化器的元素数量为 2Φ 。在混合精度训练中，会使用半精度来进行前向与反向传播计算，优化器更新模型参数时会使用单精度进行状态、梯度以及参数的更新。所以一个参数在训练时占用的空间为正向传播时使用半精度和反向传播时使用单精度所占用的空间之和。因此，使用AdamW优化器和混合精度训练来训练时候，针对每个可训练模型参数，训练阶段会占用 (2+4)+(2+4)+(4+4)=20bytes  。参数量为 Φ 的大模型，模型参数、梯度和优化器状态占用的显存大小为 20Φ bytes 。
3.jpeg

模型参数、梯度与优化器状态的空间占用已经计算完了，接下来就是在前向传播时的中间激活部分的空间占用。我们将在后续小节进行分析。
模型的训练包含 Forward 和 Backward 过程。Backward 过程实际上包含两部分，一部分是对输入的梯度（链式法则），一部分是对权重的梯度。其实这两部分主要的计算量都是矩阵乘法，并且大小与 Forward中的大小一致，因此往往会直接近似 Backward 的计算量为 Forward 的 2 倍。
3.2 推理

推理阶段通常比训练阶段要求更低的显存，因为不涉及梯度计算和参数更新等大量计算。少了梯度、优化器状态和中间激活，模型推理阶段占用的显存要远小于训练阶段。
如果使用KV cache来加速推理过程，KV cache也需要占用显存，KV cache占用的显存下文会详细介绍，此处忽略。此外，输入数据也需要放到GPU上，还有一些中间结果（推理过程中的中间结果用完会尽快释放掉），不过这部分占用的显存是很小的，也可以忽略。
最终，推理阶段的主要显存占用为模型的参数，模型参数内存 = n × p。n是模型参数总量，p是每个参数占用的字节数。如果使用半精度进行推理的话，一个参数占用2bytes空间，那么模型在推理时的显存占用约为：

\[mem_{inference} = 2 \times n_{params}\]
以下是计算模型推理时所需显存的一些关键因素：

  • 模型结构： 模型的结构包括层数、每层的神经元数量、卷积核大小等。较深的模型通常需要更多的显存，因为每一层都会产生中间计算结果。
  • 输入数据： 推理时所需的显存与输入数据的尺寸有关。更大尺寸的输入数据会占用更多的显存。
  • 批处理大小 BatchSize： 批处理大小是指一次推理中处理的样本数量。较大的批处理大小可能会增加显存使用，因为需要同时存储多个样本的计算结果。
  • 数据类型： 使用的数据类型（如单精度浮点数、半精度浮点数）也会影响显存需求。较低精度的数据类型通常会减少显存需求。
  • 中间计算： 在模型的推理过程中，可能会产生一些中间计算结果，这些中间结果也会占用一定的显存。
3.3 激活

训练中的激活（activations）指的是：前向传播过程中计算得到的，并在反向传播过程中需要用到的所有张量。这里的激活不包含模型参数和优化器状态，但包含了dropout操作需要用到的mask矩阵。
在一次训练迭代中，模型参数（或梯度）占用的显存大小只与模型参数量和参数数据类型有关，与输入数据的大小是没有关系的。优化器状态占用的显存大小也是一样，与优化器类型有关，与模型参数量有关，但与输入数据的大小无关。而中间激活值与输入数据的大小（批次大小 b 和序列长度 s ）是成正相关的，随着批次大小 b 和序列长度 s 的增大，中间激活占用的显存会同步增大。当我们训练神经网络遇到显存不足OOM（Out Of Memory）问题时，通常会尝试减小批次大小来避免显存不足的问题，这种方式减少的其实是中间激活占用的显存，而不是模型参数、梯度和优化器的显存。
我们接下来以论文“Reducing Activation Recomputation in Large Transformer Models”中的Megatron为例，分步来计算一下中间激活的显存占用。
架构

下图就是Megatron的架构。
4.jpeg

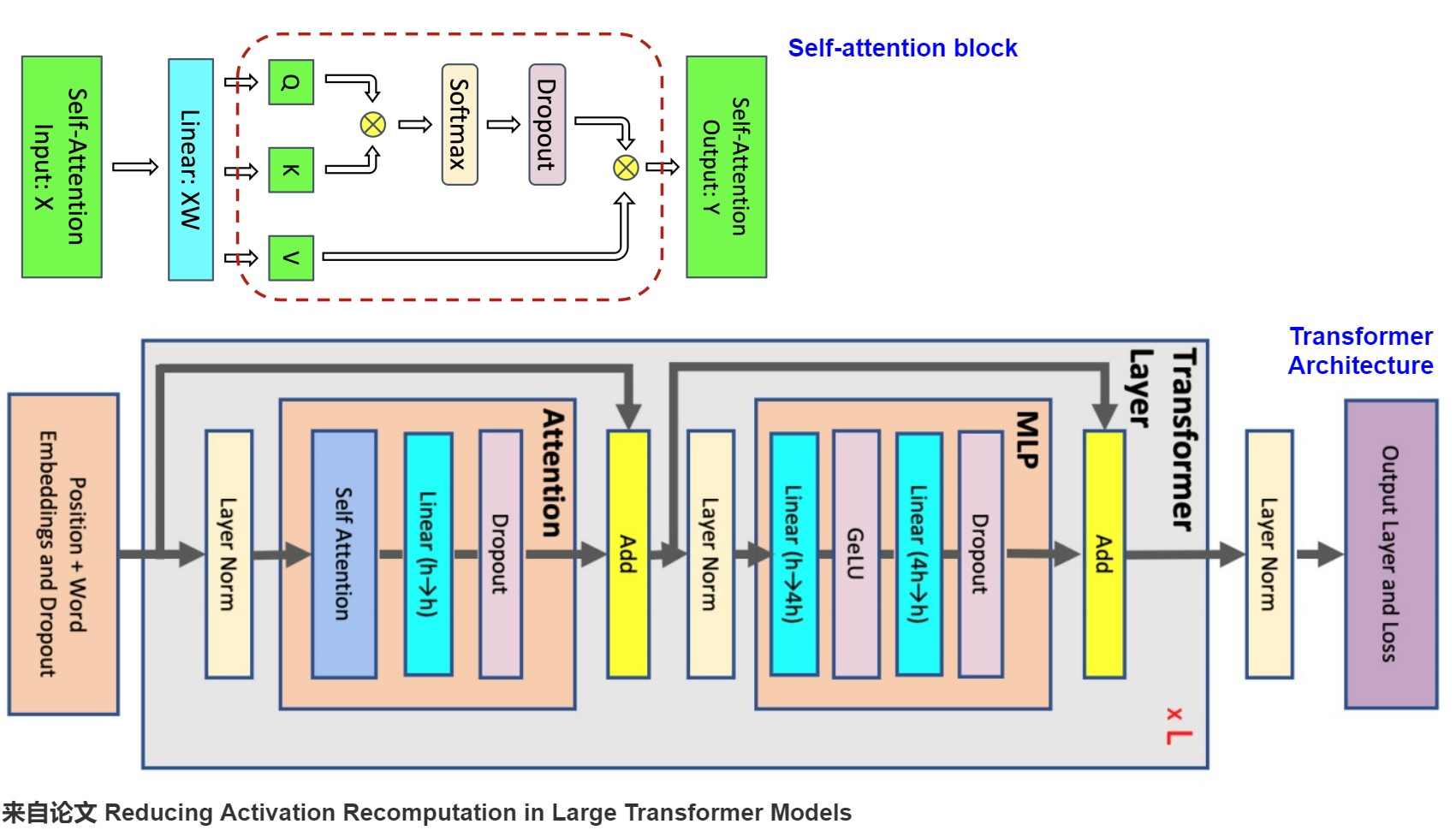
其代码如下所示。其中指定了core_attention就是submodules.core_attention，linear_proj就是submodules.linear_proj。
  1. class Attention(MegatronModule, ABC):
  2.     """Attention layer abstract class.
  3.     This layer only contains common modules required for the "self attn" and
  4.     "cross attn" specializations.
  5.     """
  6.     def __init__(
  7.         self,
  8.         config: TransformerConfig,
  9.         submodules: Union[SelfAttentionSubmodules, CrossAttentionSubmodules],
  10.         layer_number: int,
  11.         attn_mask_type: AttnMaskType,
  12.         attention_type: str,
  13.     ):
  14.         super().__init__(config=config)
  16.         self.config = config
  17.         self.layer_number = layer_number
  18.         self.attn_mask_type = attn_mask_type
  19.         self.attention_type = attention_type
  21.         # For normal attention without groups, num_query_groups == num_attention_heads,
  22.         # so these two will be the same
  23.         self.query_projection_size = self.config.kv_channels * self.config.num_attention_heads
  24.         self.kv_projection_size = self.config.kv_channels * self.config.num_query_groups
  26.         # Per attention head and per partition values.
  27.         world_size = parallel_state.get_tensor_model_parallel_world_size()
  28.         self.hidden_size_per_attention_head = divide(
  29.             self.query_projection_size, self.config.num_attention_heads
  30.         )
  31.         self.num_attention_heads_per_partition = divide(self.config.num_attention_heads, world_size)
  32.         self.num_query_groups_per_partition = divide(self.config.num_query_groups, world_size)
  34.         self.core_attention = build_module(
  35.             submodules.core_attention,
  36.             config=self.config,
  37.             layer_number=self.layer_number,
  38.             attn_mask_type=self.attn_mask_type,
  39.             attention_type=self.attention_type,
  40.         )
  42.         self.checkpoint_core_attention = self.config.recompute_granularity == 'selective'
  44.         # Output.
  45.         self.linear_proj = build_module(
  46.             submodules.linear_proj,
  47.             self.query_projection_size,
  48.             self.config.hidden_size,
  49.             config=self.config,
  50.             init_method=self.config.output_layer_init_method,
  51.             bias=self.config.add_bias_linear,
  52.             input_is_parallel=True,
  53.             skip_bias_add=True,
  54.             is_expert=False,
  55.             tp_comm_buffer_name='proj',
  56.         )
  57.         
  58.         
  59.     def forward(
  60.         self,
  61.         hidden_states,
  62.         attention_mask,
  63.         key_value_states=None,
  64.         inference_params=None,
  65.         rotary_pos_emb=None,
  66.         packed_seq_params=None,
  67.     ):
  68.         # hidden_states: [sq, b, h]
  70.         # For self attention we just duplicate the rotary_pos_emb if it isn't already
  71.         if rotary_pos_emb is not None and not isinstance(rotary_pos_emb, tuple):
  72.             rotary_pos_emb = (rotary_pos_emb,) * 2
  74.         # =====================
  75.         # Query, Key, and Value
  76.         # =====================
  77.         # Get the query, key and value tensors based on the type of attention -
  78.         # self or cross attn.
  79.         query, key, value = self.get_query_key_value_tensors(hidden_states, key_value_states)
  81.         # ===================================================
  82.         # Adjust key, value, and rotary_pos_emb for inference
  83.         # ===================================================
  84.         key, value, rotary_pos_emb, attn_mask_type = self._adjust_key_value_for_inference(
  85.             inference_params, key, value, rotary_pos_emb
  86.         )
  88.         if packed_seq_params is not None:
  89.             query = query.squeeze(1)
  90.             key = key.squeeze(1)
  91.             value = value.squeeze(1)
  93.         # ================================================
  94.         # relative positional embedding (rotary embedding)
  95.         # ================================================
  96.         if rotary_pos_emb is not None:
  97.             q_pos_emb, k_pos_emb = rotary_pos_emb
  99.             if packed_seq_params is not None:
  100.                 cu_seqlens_q = packed_seq_params.cu_seqlens_q
  101.                 cu_seqlens_kv = packed_seq_params.cu_seqlens_kv
  102.             else:
  103.                 cu_seqlens_q = cu_seqlens_kv = None
  104.             query = apply_rotary_pos_emb(
  105.                 query, q_pos_emb, config=self.config, cu_seqlens=cu_seqlens_q
  106.             )
  107.             key = apply_rotary_pos_emb(key, k_pos_emb, config=self.config, cu_seqlens=cu_seqlens_kv)
  109.             # TODO, can apply positional embedding to value_layer so it has
  110.             # absolute positional embedding.
  111.             # otherwise, only relative positional embedding takes effect
  112.             # value_layer = apply_rotary_pos_emb(value_layer, k_pos_emb)
  114.         # ==================================
  115.         # core attention computation
  116.         # ==================================
  118.         if self.checkpoint_core_attention and self.training:
  119.             core_attn_out = self._checkpointed_attention_forward(
  120.                 query,
  121.                 key,
  122.                 value,
  123.                 attention_mask,
  124.                 attn_mask_type=attn_mask_type,
  125.                 packed_seq_params=packed_seq_params,
  126.             )
  127.         else:
  128.             core_attn_out = self.core_attention(
  129.                 query,
  130.                 key,
  131.                 value,
  132.                 attention_mask,
  133.                 attn_mask_type=attn_mask_type,
  134.                 packed_seq_params=packed_seq_params,
  135.             )
  137.         if packed_seq_params is not None:
  138.             # reshape to same output shape as unpacked case
  139.             # (t, np, hn) -> (t, b=1, h=np*hn)
  140.             # t is the pack size = sum (sq_i)
  141.             # note that batch is a dummy dimension in the packed case
  142.             core_attn_out = core_attn_out.reshape(core_attn_out.size(0), 1, -1)
  144.         # =================
  145.         # Output. [sq, b, h]
  146.         # =================
  148.         output, bias = self.linear_proj(core_attn_out) # 这里是线性层
  150.         return output, bias
复制代码
最终注意力代码是：
  1. class DotProductAttention(MegatronModule):
  2.     """
  3.     Region where selective activation recomputation is applied.
  4.     This region is memory intensive but less compute intensive which
  5.     makes activation checkpointing more efficient for LLMs (20B+).
  6.     See Reducing Activation Recomputation in Large Transformer Models:
  7.     https://arxiv.org/abs/2205.05198 for more details.
  9.     We use the following notation:
  10.      h: hidden size
  11.      n: number of attention heads
  12.      p: number of tensor model parallel partitions
  13.      b: batch size
  14.      s: sequence length
  15.     """
  17.     def __init__(
  18.         self,
  19.         config: TransformerConfig,
  20.         layer_number: int,
  21.         attn_mask_type: AttnMaskType,
  22.         attention_type: str,
  23.         attention_dropout: float = None,
  24.     ):
  25.         super().__init__(config=config)
  27.         self.config: TransformerConfig = config
  29.         assert (
  30.             self.config.context_parallel_size == 1
  31.         ), "Context parallelism is only supported by TEDotProductAttention!"
  33.         assert (
  34.             self.config.window_size is None
  35.         ), "Sliding Window Attention is only supported by TEDotProductAttention!"
  37.         self.layer_number = max(1, layer_number)
  38.         self.attn_mask_type = attn_mask_type
  39.         self.attention_type = attention_type  # unused for now
  41.         projection_size = self.config.kv_channels * self.config.num_attention_heads
  43.         # Per attention head and per partition values.
  44.         world_size = parallel_state.get_tensor_model_parallel_world_size()
  45.         self.hidden_size_per_partition = divide(projection_size, world_size)
  46.         self.hidden_size_per_attention_head = divide(projection_size, config.num_attention_heads)
  47.         self.num_attention_heads_per_partition = divide(self.config.num_attention_heads, world_size)
  48.         self.num_query_groups_per_partition = divide(self.config.num_query_groups, world_size)
  50.         coeff = None
  51.         self.norm_factor = math.sqrt(self.hidden_size_per_attention_head)
  52.         if self.config.apply_query_key_layer_scaling:
  53.             coeff = self.layer_number
  54.             self.norm_factor *= coeff
  56.         self.scale_mask_softmax = FusedScaleMaskSoftmax(
  57.             input_in_fp16=self.config.fp16,
  58.             input_in_bf16=self.config.bf16,
  59.             attn_mask_type=self.attn_mask_type,
  60.             scaled_masked_softmax_fusion=self.config.masked_softmax_fusion,
  61.             mask_func=attention_mask_func,
  62.             softmax_in_fp32=self.config.attention_softmax_in_fp32,
  63.             scale=coeff,
  64.         )
  66.         # Dropout. Note that for a single iteration, this layer will generate
  67.         # different outputs on different number of parallel partitions but
  68.         # on average it should not be partition dependent.
  69.         self.attention_dropout = torch.nn.Dropout(
  70.             self.config.attention_dropout if attention_dropout is None else attention_dropout
  71.         )
  73.     def forward(
  74.         self,
  75.         query: Tensor,
  76.         key: Tensor,
  77.         value: Tensor,
  78.         attention_mask: Tensor,
  79.         attn_mask_type: AttnMaskType = None,
  80.         packed_seq_params: Optional[PackedSeqParams] = None,
  81.     ):
  82.         assert packed_seq_params is None, (
  83.             "Packed sequence is not supported by DotProductAttention."
  84.             "Please use TEDotProductAttention instead."
  85.         )
  87.         # ===================================
  88.         # Raw attention scores. [b, n/p, s, s]
  89.         # ===================================
  91.         # expand the key and value [sk, b, ng, hn] -> [sk, b, np, hn]
  92.         # This is a noop for normal attention where ng == np. When using group query attention this
  93.         # creates a view that has the keys and values virtually repeated along their dimension to
  94.         # match the number of queries.
  96.         # attn_mask_type is not used.
  97.         if self.num_attention_heads_per_partition // self.num_query_groups_per_partition > 1:
  98.             key = key.repeat_interleave(
  99.                 self.num_attention_heads_per_partition // self.num_query_groups_per_partition, dim=2
  100.             )
  101.             value = value.repeat_interleave(
  102.                 self.num_attention_heads_per_partition // self.num_query_groups_per_partition, dim=2
  103.             )
  105.         # [b, np, sq, sk]
  106.         output_size = (query.size(1), query.size(2), query.size(0), key.size(0))
  108.         # [sq, b, np, hn] -> [sq, b * np, hn]
  109.         # This will be a simple view when doing normal attention, but in group query attention
  110.         # the key and value tensors are repeated to match the queries so you can't use
  111.         # simple strides to extract the queries.
  112.         query = query.reshape(output_size[2], output_size[0] * output_size[1], -1)
  113.         # [sk, b, np, hn] -> [sk, b * np, hn]
  114.         key = key.view(output_size[3], output_size[0] * output_size[1], -1)
  116.         # preallocting input tensor: [b * np, sq, sk]
  117.         matmul_input_buffer = parallel_state.get_global_memory_buffer().get_tensor(
  118.             (output_size[0] * output_size[1], output_size[2], output_size[3]), query.dtype, "mpu"
  119.         )
  121.         # Raw attention scores. [b * np, sq, sk]
  122.         matmul_result = torch.baddbmm(
  123.             matmul_input_buffer,
  124.             query.transpose(0, 1),  # [b * np, sq, hn]
  125.             key.transpose(0, 1).transpose(1, 2),  # [b * np, hn, sk]
  126.             beta=0.0,
  127.             alpha=(1.0 / self.norm_factor),
  128.         )
  130.         # change view to [b, np, sq, sk]
  131.         attention_scores = matmul_result.view(*output_size)
  133.         # ===========================
  134.         # Attention probs and dropout ----------------- 在这里有softmax的dropout
  135.         # ===========================
  137.         # attention scores and attention mask [b, np, sq, sk]
  138.         attention_probs: Tensor = self.scale_mask_softmax(attention_scores, attention_mask)
  140.         # This is actually dropping out entire tokens to attend to, which might
  141.         # seem a bit unusual, but is taken from the original Transformer paper.
  143.         if not self.config.sequence_parallel:
  144.             with tensor_parallel.get_cuda_rng_tracker().fork():
  145.                 attention_probs = self.attention_dropout(attention_probs)
  146.         else:
  147.             attention_probs = self.attention_dropout(attention_probs)
  149.         # =========================
  150.         # Context layer. [sq, b, hp]
  151.         # =========================
  153.         # value -> context layer.
  154.         # [sk, b, np, hn] --> [b, np, sq, hn]
  156.         # context layer shape: [b, np, sq, hn]
  157.         output_size = (value.size(1), value.size(2), query.size(0), value.size(3))
  159.         # change view [sk, b * np, hn]
  160.         value = value.view(value.size(0), output_size[0] * output_size[1], -1)
  162.         # change view [b * np, sq, sk]
  163.         attention_probs = attention_probs.view(output_size[0] * output_size[1], output_size[2], -1)
  165.         # matmul: [b * np, sq, hn]
  166.         context = torch.bmm(attention_probs, value.transpose(0, 1))
  168.         # change view [b, np, sq, hn]
  169.         context = context.view(*output_size)
  171.         # [b, np, sq, hn] --> [sq, b, np, hn]
  172.         context = context.permute(2, 0, 1, 3).contiguous()
  174.         # [sq, b, np, hn] --> [sq, b, hp]
  175.         new_context_shape = context.size()[:-2] + (self.hidden_size_per_partition,)
  176.         context = context.view(*new_context_shape)
  178.         return context
复制代码
术语说明

我们首先看看论文中的术语。

  • a是 transformer 模型中注意力头 (attention heads) 的个数。
  • b为每个GPU的batch size；
  • h是每个 transformer 层的隐含维度
  • L为Transformer的层数；
  • p为流水线并行的并行机器数；
  • s为句子的长度，即序列中词元的个数
  • t为张量并行的并行机器数；
  • v为词典的大小；
我们假设激活数据类型为 fp16。
数据量

每个Transformer层由一个注意力和一个MLP构成，中间还有两个LayerNorm。下面，我们来推导存储每个元素的激活所需的内存。在下面的分析中需要注意几点：

  • 单位是bytes，而不是元素个数。
  • 大模型在训练过程中通常采用混合精度训练，因此，在分析中间激活的显存占用时，我们假设中间激活值是以float16或bfloat16数据格式来保存的，每个元素占了2个bytes。唯一例外的是，dropout操作的mask矩阵，每个元素只占1个bytes。
  • 在分析中间激活的显存占用时，只考虑激活占用显存的大头，忽略掉一些小的buffers。比如，对于layer normalization，计算梯度时需要用到层的输入、输入的均值 和方差 。输入包含了 bsℎ 个元素，而输入的均值和方差分别包含了 bs 个元素。由于 ℎ 通常是比较大的（千数量级），有 bsℎ≫bs 。因此，对于layer normalization，中间激活近似估计为 bsℎ ，而不是 bsℎ+2bs 。
注意力块

注意力块的激活如下。
保存内容操作激活大小所属模块保存原因XQuery (Q), Key (K), Value (V) 相关的矩阵乘法2bshself attention保存Q/K/V共同的输入XQ、K\(QK^T\) 矩阵乘法4bshself attention保存 \(QK^T\) 矩阵乘法的输入\(QK^T\)Softmax\(2 bas^2\)self attention保存Softmax 的输入，形状是 [b, a, s, s]MaskSoftmax dropout\(bas^2\)self attention保存Softmax dropout 的mask，形状和\(QK^T\)相同，一个byte即可V注意力计算2bshself attention保存\(softmax(\frac{QK^T}{\sqrt d})V\)的输入VScore注意力计算\(2 bas^2\)self attention保存\(softmax(\frac{QK^T}{\sqrt d})V\)的输入\(softmax(\frac{QK^T}{\sqrt d})\)Linear计算输出映射2bshlinear projection输入映射需要保存其输入Maskattention dropoutbshattention dropout24内dropout需要保存mask矩阵，一个byte即可总计\(11bsh + 5bas^2\)我们回顾一下MHA的计算逻辑如下：

\[MultiHead(Q,K,V)=Concat(head_1,head_2,...,head_{n_{heads}})W_O \\where\ head_i = Attention(QW^Q_i, KW^K_i, VW^V_i) \\=softmax(\frac{QW^Q_i(KW_i^K)^T}{\sqrt d_{head}}) VW^V_i\]
上述表格中的各个计算解释如下。

  • 输入X。X被用来计算Q、K、V。X的形状是[b,s,h]，元素个数是bsh，FP16占据两个byte，所以显存为2bsh。
  • 中间激活 Q、K。这两者被用来计算\(QK^T\)。Q、K的形状都是[b,s,h]，元素类型是FP16，两者占据显存大小是4bsh。
  • 中间激活\(QK^T\)。\(QK^T\)是softmax的输入，元素类型是FP16，占据显存大小是\(2bs^2a\)。a是注意力头数目。
    Q的形状是[b,a,s,h/a]，\(K^T\)形状是[b,a,h/a,s]。\(QK^T\)形状是[b,a,s,s]。计算公式如下：\(score=softmax(QK^T/\sqrt d_k)\)
  • dropout用到的mask矩阵。softmax操作完成之后，会进行dropout操作。需要保存一个mask矩阵，mask矩阵的形状与\(QK^T\)相同，类型是int，占据显存是\(bs^2a\)。
  • score权重矩阵和V。这两者被用来计算Z。

    • softmax和dropout结束之后，得到了score权重矩阵，大小是2\(bs^2a\)。
    • V的形状都是[b,s,h]，元素类型是FP16，占据显存大小是2bsh。

  • 计算输出映射以及一个dropout操作。输入映射需要保存其输入，大小为 2bsh ；dropout需要保存mask矩阵，大小为 bsh 。二者占用显存大小合计为 3bsh。
因此，将上述中间激活相加得到self-attention块的中间激活占用显存大小为 \(11bsh + 5bas^2\)
MLP

FFN的两个线性层以2sbh和8sbh的大小存储它们的输入。GeLU非线性还需要其大小为8sbh的输入用于反向传播。最后，dropout将其掩码存储为sbh大小。总的来说，MLP块需要19sbh字节的存储空间。
模块动作激活大小linear 1第一个线性层需要保存其输入2 bshGeLU激活函数需要保存其输入8 bshlinear 2第二个线性层需要保存其输入8 bshdropout最后有一个dropout操作，需要保存mask矩阵bsh总计19sbh我们回顾一下MHA的计算逻辑如下：

\[FFN(x) = f_{gelu}(xW_1+b_1)W_2 + b_2\]
上述的各个计算如下。

  • 第一个线性层需要保存其输入，占用显存大小为 2bsh 。
  • 激活函数需要保存其输入，占用显存大小为 8bsh 。
  • 第二个线性层需要保存其输入，占用显存大小为 8bsh。
  • 最后有一个dropout操作，需要保存mask矩阵，占用显存大小为bsh 。
因此，对于MLP块，需要保存的中间激活值为 19bsh 。
LayerNorm

另外，self-attention块和MLP块分别对应了一个layer normalization。每个layer norm需要保存其输入，大小为 2sbh。2个layer norm需要保存的中间激活为 4sbh。
总结

综上，每个transformer层需要保存的中间激活占用显存大小为\(34bsh + 5bas^2\)。对于 l 层transformer模型，还有embedding层、最后的LayerNorm和输出层。当隐藏维度 ℎ 比较大，层数l 较深时，这部分的中间激活是很少的，可以忽略。因此，对于 l 层transformer模型，中间激活占用的显存大小可以近似为   \((34bsh + 5bas^2)\times l\)。
作为对比，下图是哈佛代码中解码器对应的激活情况，里面有各个张量的形状。
5.jpeg

有研究指出，13B 的 LLM 推理时，每个 token 大约消耗 1MB 的显存。
另外，对于计算量和显存量，我们也很容易见到不同的计算结果，这基本是因为计算原则不同，比如：梯度可能是FP16存储，参数可能是FP32存储，是否采用重计算等等。
并行

实际工作中，LLM总是以各种并行策略进行训练或者推理，激活又各不相同。下图是各种并行策略下，每个Transfromer层的激活大小（bytes）。
6.jpeg

我们再来看看并行策略下，对于 l 层transformer模型，embedding层、最后的LayerNorm和输出层所输出的激活。

  • 位置和单词嵌入不需要为反向传播存储任何大量的激活。但是dropout需要存储。嵌入层中的dropout也会沿着序列维度进行并行（sequence parallelism）。因此，它的存储将占据sbhp/t大小。请注意，系数p是因为流水线并行中，我们需要存储p个microbatches（微批次）。
  • 输出层之前的Layer Norm也使用序列并行（sequence parallelism），因此需要2sbh/t存储。输出层会投影到词汇表维度，这需要存储大小为2sbh/t的输入。最后，交叉熵损失（cross entropy loss）需要存储以32位浮点进行计算的logit，因此需要4sbv/t的存储空间。请注意，由于我们只考虑流水线第一阶段的激活，因此上述激活，即总共4sbh/t(1+v/h)，仅在没有流水线并行（p=1）的情况下才会考虑在内。
  • 输入嵌入、最后一个LayerNorm和输出层而产生的总共额外内存为：
    7.jpeg

0x04 Transformer计算量

广义上，当处理一个 token 时，模型执行两种类型的操作：注意力计算和矩阵-向量乘法。

  • MHA（红框）：\(W_Q\)，\(W_K\)，\(W_V\) 对应的计算量都为 2 x (d x d x l)，其中 2 表示一个乘法和一个加法。
  • MHA（蓝框）：\(W_{out}\) 对应的计算量为 2 x (d x d x l)。
  • MHA Attention（绿色圆角方块）：计算量是2 x (l x d/h x l + l x d/h x l) x h = 4 x d x l x l。如果是 Decoder（LLM），由于 Causal Mask 的存在，此处的计算量应该减半，也就是 2 x d x l x l。
  • FFN（绿框）：W1 和 W2 对应的计算量为 $2 \times  (d_{FFN} \times  d \times  l) $和 \(2\times  (d \times  _{FFN} \times  l)\)。LLaMA 的 SwiGLU 类似。
8.jpeg

我们后续也按照megatron论文的术语进行分析，忽略多头，即头数为1。
4.1 矩阵乘法

在decode阶段，则主要是矩阵-向量乘法。一个大矩阵乘以一个向量，得到另一个向量。
因此我们首先看看矩阵乘法的计算特点。人们定义算术强度（Arithmetic Intensity）为FLOP : I/O。当将一个\(N\times M\)矩阵与一个\(M\times P\)矩阵相乘以产生一个\(N\times P\)矩阵时，矩阵-向量乘法对每个矩阵元素执行一次乘加运算。FLOP（浮点操作，即计算量）为\(2M\times P \times N\)，I/O（从GPU内存传输到GPU寄存器的数据传输）计数为\(M\times N + M \times P + N \times P\) 。
4.2 前向传播计算量

Embedding

Embedding操作的输入是[b,s]。在实际计算的矩阵-向量乘法中，embedding操作并不会使用这整个embedding大矩阵，每个 token 只读取这个矩阵中的一行，就是查表操作。最终输出张量变成[b,s,h]。因此计算量相对很小，后面我们将忽略这部分。
MHA

在标准的Transformer计算中，假设\(Q,K,V \in R^{s\times h}\)，则计算如下（省略了\(\sqrt h\)）。N是序列长度，h是维度。

  • 获取注意力分数 ：$ S = QK^T \in R^{s \times s}$。对每个 query 向量，都计算它与所有位置的 key 向量之间的点积。
  • 获取注意力权重：$ P = softmax(S) \in R^{s \times s}$。即归一化得到的一组标量。
  • 计算最终输出：\(O = PV \in R^{s \times h}\)。使用注意力权重，对所有之前的 value 向量进行加权求和来计算一个向量o。
因此我们可以知道，计算S和O是主要的部分。
计算Q、K、V

单个矩阵乘法是：[b, s, h] x [h, h] 得到 [b, s, h]，因此其计算量是\(2bsh^2\)。三个矩阵的计算量是 \(3 \times 2 bsh^2 = 6 bsh^2\)
QK^T

在这个阶段，针对每个query元素，注意力计算会对每个键元素执行一次乘加操作以计算点积。总体操作为：[b,  s, h] x [b,  h, s] = [b, s, s] ，其计算量是：\(2bs^2h\)

softmax 函数不会改变输入矩阵的维度，即 [
来源：程序园用户自行投稿发布，如果侵权，请联系站长删除
免责声明：如果侵犯了您的权益，请联系站长，我们会及时删除侵权内容，谢谢合作！

使用道具 举报
相关推荐
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 立即注册
发帖
悯拄等
4 天前

0

粉丝关注

12

主题发布

板块介绍填写区域，请于后台编辑
微信扫一扫